优化算法学习总结

1. 动量梯度下降

为了解决随机梯度梯度下降存在的震荡问题，通过添加动量，平滑动量变化。

什么是指数加权平均

当前步的函数值不仅取决于当前的输入，还取决于之前的函数值，公式如下

$$v_t = \beta v_{t-1}+(1-\beta)\theta_t$$

通过不断带入展开，可得只包含 $\theta$ 的表达式为

$$v_t = (1-\beta)\theta_t + (1-\beta)\beta\theta_{t-1} + (1-\beta)\beta^2\theta_{t-2}+....+(1-\beta)\beta^n\theta_{t-n}+\beta^nv_{t-n}$$

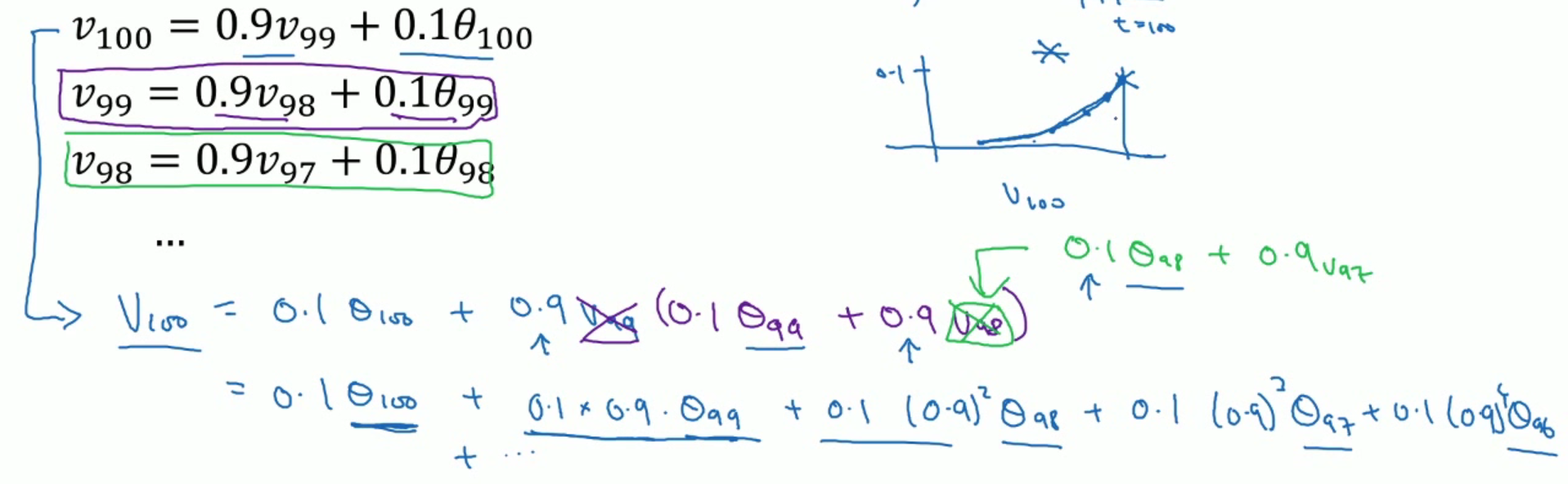
由于 $(1-\frac{1}{n})^n$ 在n趋向于无穷时等于 $e^{-1}$。当 $\beta$ 趋向于1时，$\beta^{\frac{1}{1-\beta}} = (1-\frac{1}{n})^n$ 同样等于 $e^{-1}$,如果将 $e^{-1}$看作一个可以忽略的数字，则展开式中含有阶数大于等于 $\theta^{\frac{1}{1-\theta}}$ 的相可以忽略。

• 当 $\beta = 0.98$​时，$\beta^{\frac{1}{1-\beta}} = \beta^{20}$​ ,所以所有系数包含$\beta^n$​ n>=20的均省略，原式子等价于前20个$\theta$​的加权平均和，即当前梯度等于前20个梯度的加权平均和

动量梯度下降公式

假设第 $t$ 次训练的输入为 $x_t$ ,学习率为$\eta_t$,计算得到梯度为 $g_t$ ,并定义速度向量 $v_t$,初始化为0；动量系数为m

$$v_t = m * v_{t-1} + \eta * g_t \\ x_t = x_{t-1} - v_t$$

其中 $0<m<1$，当 $m=0$ 时等价于随机梯度下降

通过对历史梯度进行指数加权平均，实现了梯度的平滑变换，确保了相邻梯度方向的一致性，解决了梯度下降的震荡问题。

2. AdaGrad算法

为解决不同方向梯度大小变化不同，导致学习率设置的问题，adagrad算法根据每个方向梯度大小，不断更新学习率

AdaGrad公式

首先定义向量 $s_t$ ,初始化为0，每次迭代累加梯度的内积，递归公式为

$$s_t = s_{t-1} + g_i * g_i$$

更新目标参数是，使用 $s_t$ 更新学习率大小,其中 $\epsilon$ 为为保持数值稳定性添加的常数

$$x_t = x_{t-1} - \frac{\eta}{\sqrt{s_t+\epsilon}}*g_t$$

AdaGrad算法能够根据梯度大小设置学习率，梯度越大，学习率越小，但是由于 $s_t$ 为累加形式，学习率随着训练会不断减小，到后期学习速率可能过慢

3. RMSprop算法

为了解决AdAGrad算法后期，学习率过小可能无法找到最优解的问题，在计算 $s_t$ 时引入加权平均

RMSprop公式

引入加权平均后的 $s_t$ 计算公式如下，避免了学习率的不断减小

$$s_t = \theta s_{t-1} + (1-\theta)g_i * g_i$$

4. AdaDelta算法

舍弃了学习率这一参数，从另一个角度解决AdaGrad后期学习率变小，难以找到最优解的问题

AdaDelta公式

$s_t$递推公式与RMSprop一致

$$s_t = \theta s_{t-1} + (1-\theta)g_i * g_i$$

增加了状态 $\Delta x_t$,计算梯度 $g’_t$

$$g'_t = \sqrt{\frac{\Delta x_{t-1} + \epsilon}{s_t + \epsilon}}*g_t$$

使用 $g’_t$ 更新参数

$$x_t = x_{t-1} - g'_t$$

其中状态 $\Delta x_t$ 的递推公式为

$$\Delta x_t = \theta \Delta x_{t-1} + (1-\theta)g'_i * g'_i$$

与RMSprop算法区别点在于学习率也通过指数加权平均递归计算

5. Adam算法

Adam算法结合了动量法和RMSprop法，对梯度和$s_t$ 均进行了指数加权平均

$s_t$递推公式($\theta_1$ 建议为0.999）

$$s_t = \theta_1 s_{t-1} + (1-\theta_1)g_i * g_i$$

$v_t$ 递推公式($\theta_2$ 建议为0.9）

$$v_t = \theta_2 * v_{t-1} + \theta_2 * g_t$$

由于 $s_t$ 和 $v_t$ 在递推初始化时初始化为0，根据递推公式中 $\theta_1$ 和 $\theta_2$ 均为接近于1的数，导致在训练初期， $s_t$ 和 $v_t$ 取值与梯度关系不大，更加趋向于0，因此需要增加 误差修正(bias correction) 操作

$$s'_t = \frac{s_t}{1-\theta_1^t}\\ v'_t = \frac{v_t}{1-\theta_2^t}$$

使用修正后的两个参数计算新梯度

$$g'_t =\frac{\eta v'_t}{\sqrt{s'_t} + \epsilon}$$

更新参数公式为

$$x_t = x_{t-1} - g'_t$$

总结