语言模型
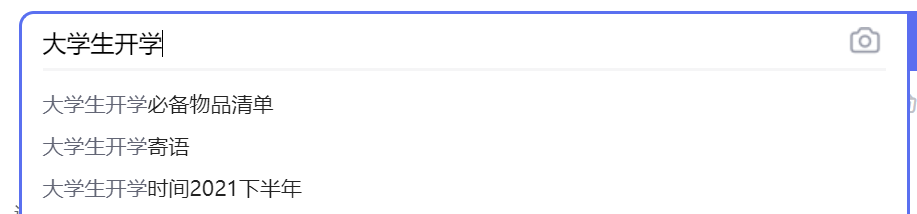
通过语言模型的构建,实现能够根据已知序列推断序列中的下一个单词,如搜索引擎中的搜索推断等。
模型的形式化定义如下,给定一系列单词,预测下一个单词的概率分布,该概率分布为当前模型词典库上词语的概率分布

条件概率角度理解语言模型形式如下,即一系列条件概率的连乘

如何构建一个语言模型(N-grams模型)
马尔可夫(Markov)假设:下一个词的出现仅仅依赖于前面的几个词,而不是整个前部分句子(简化概率计算,减少模型参数)
大数定理:在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。偶然中包含着某种必然
N-grams模型基于马尔可夫假设,指给定的一段文本或语音中N个项目(item)的序列,项目可以是音节、词语或者碱基对等,N-gram模型中的N,即对应概率依赖的词语个数,例如:
当N = 1时,1-gram模型(unigram):$p(T) = p(W1)p(W2)…..p(Wn)$ 即词语的出现相互独立
当N = 2 时,2-gram模型(bigram):$p(T) = p(W1)p(W2|W1)…..p(Wn|Wn-1)$ 即依赖前一个词语
以N-gram模型为例子,根据大数定理可得,在语料库足够大的条件下,$W_n$关于$W_1…….W_{n-1}$的条件概率为
即语料种$W_1^n$语句的出现次数除以$W_i^{n-1}$语句的次数
单词稀疏问题(Sparsity Problem)
根据N-grams的计算公式,如果语料库中不存在(或几乎没有)当前上文与目标推断单词共同出现的情况,则概率公式的分母为0,即稀疏问题,
解决方式为通过在概率公式中增加一个增量,使词库中的所有单词在给定上文预测的情况下,都具有一定的概率值(即使是不可能的单词),称之为平滑法。随着n元语法中的n不断增大,单词稀疏问题会更加严重
- Add‐One 平滑
- Add‐K 平滑
- 等
固定窗口神经网络语言模型
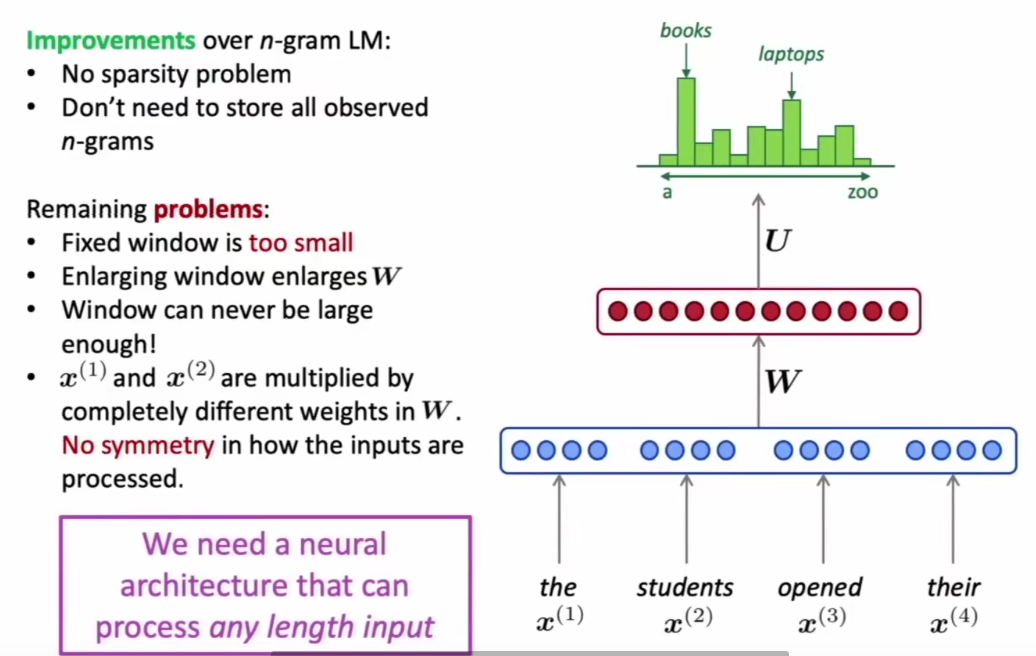
固定输入窗口大小,将输入窗口内的词语向量拼接,作为模型输入,预测下一个单词的概率,解决了非神经网络语言模型存在的单词稀疏和存储稀疏问题,但是仍存在
- 固定窗口有些时候可能太小
- 扩大窗口会导致模型参数量爆炸
- 窗口内不同位置单词对应不同的权重值(?)
基于RNN的语言模型