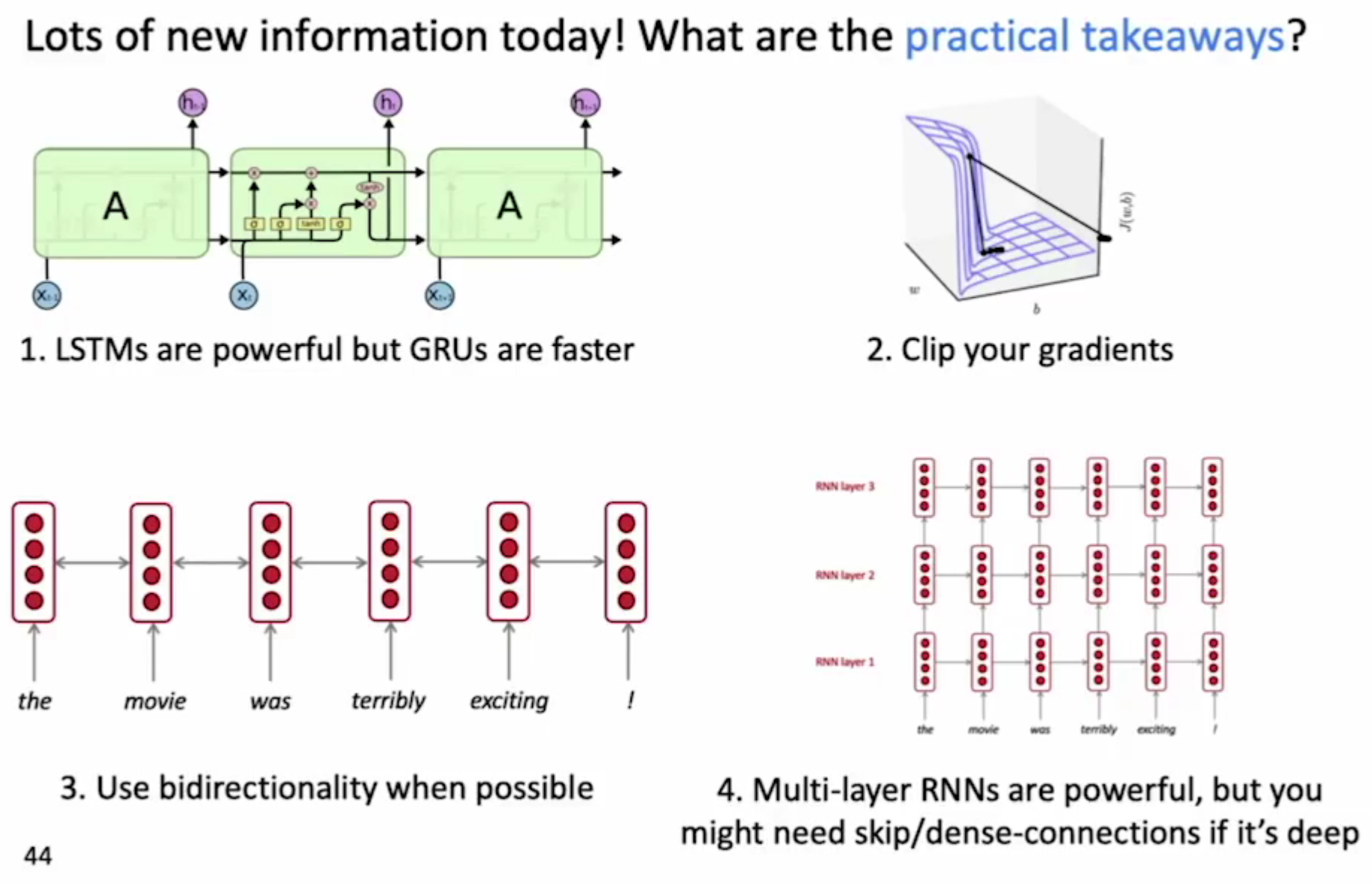
RNN梯度消失/爆炸问题(vanishing/exploding gradient problem)
由于RNN对于不同时间步的输入使用同一个神经元,在反向传播计算梯度时,随着时间步的增加,会出现梯度爆炸和消失问题

RNN时间步t计算公式为
反向传播的损失函数求导结果为
其中 $\frac{\partial s_j}{\partial S_{j-1}} = \sigma’ W_s$ (不考虑激活函数的情况下),由于累乘的性质,随着神经元系数W的累乘次数增加,如果$w$大于1,产生梯度爆炸问题;如果$w$小于,出现梯度消失问题。
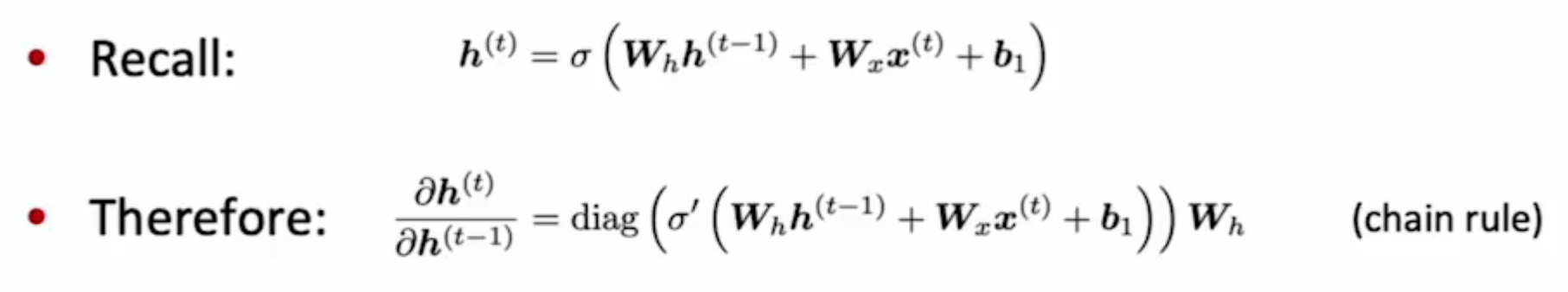
梯度消失问题导致 RNN难以捕捉长时间步距离中的有效信息


解决梯度爆炸问题
梯度剪切(clipping)

Long Short-term Memory(LSTM)
在原RNN每个时间步拥有一个隐藏状态 $h^{(t)}$ 的基础上,增加一个存储单元 $c^{(t)}$(cell state)存储RNN无法捕捉的长距离时间步信息
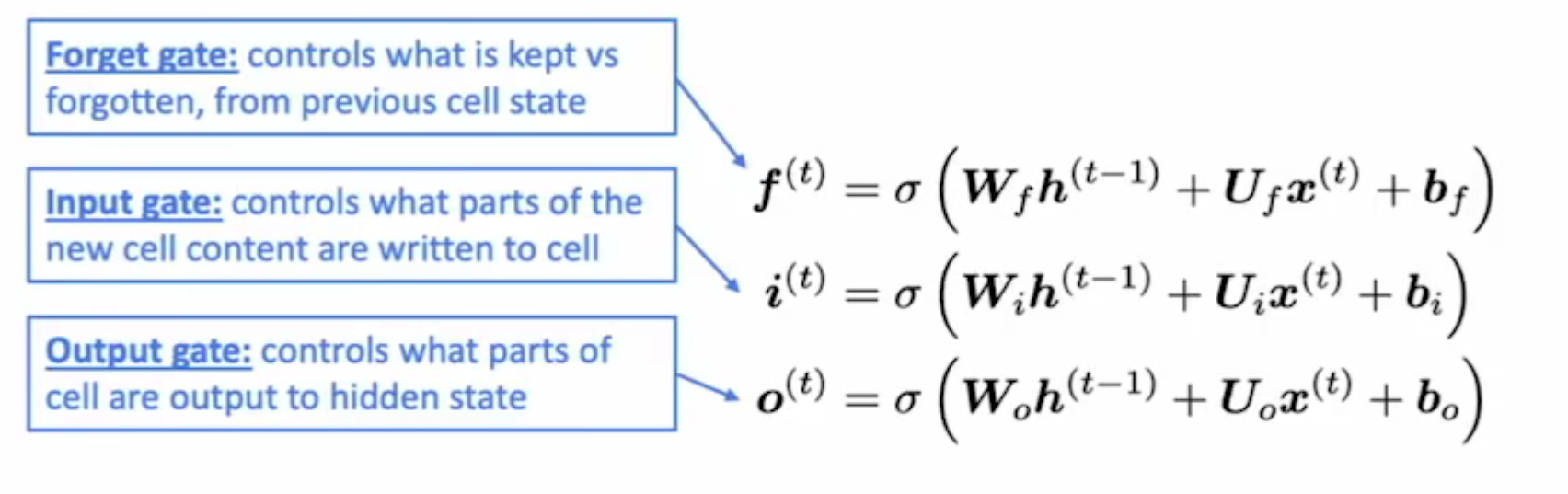
- LSTM能够从存储单元中删除、写入以及读取相关信息,是否执行这些操作由对应的控制门(gate)决定
- 每个时间步gate值由当前时间步信息动态计算
三种类型门的值均采用神经网络方式预测得到
基本计算流程:
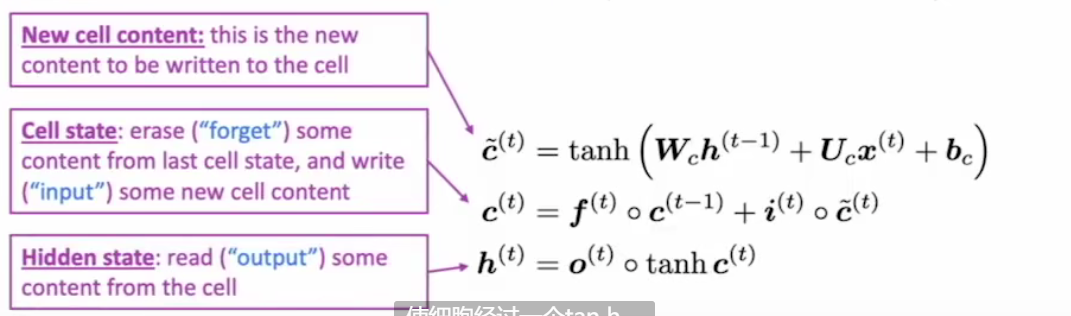
- 首先根据上一时间步隐藏状态和当前输入,计算当前存储单元候选值
- 根据遗忘门和输入门有选择的组合历史/当前存储单元计算值,获得当前存储单元值(忘记多少从前,留下多少现在)
- 根据输出门,决定隐藏状态值
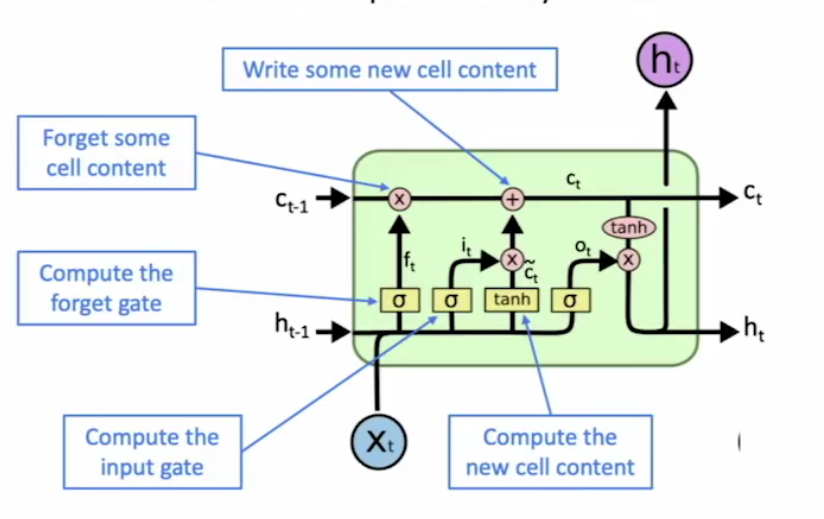
为何LSTM能够解决梯度消失问题
关注点不在于解决梯度消失或者梯度爆炸,在于解决由梯度消失带来的 长距离信息无法捕捉的问题(不解决因,而改善果),类似于resnet中的残差思路

Gated Recurrent Units(GRU) - 降低了LSTM的复杂度
不使用cell存储单元,只采用们的思想控制历史隐藏状态以及当前隐藏状态对于结果的影响。、
- $u^t$ 更新门:控制当前生成当前隐藏状态时保留的历史状态和当前隐藏状态的比例
- $r^t$ 重置门:历史隐藏状态信息 流入 当前候选隐藏状态的量
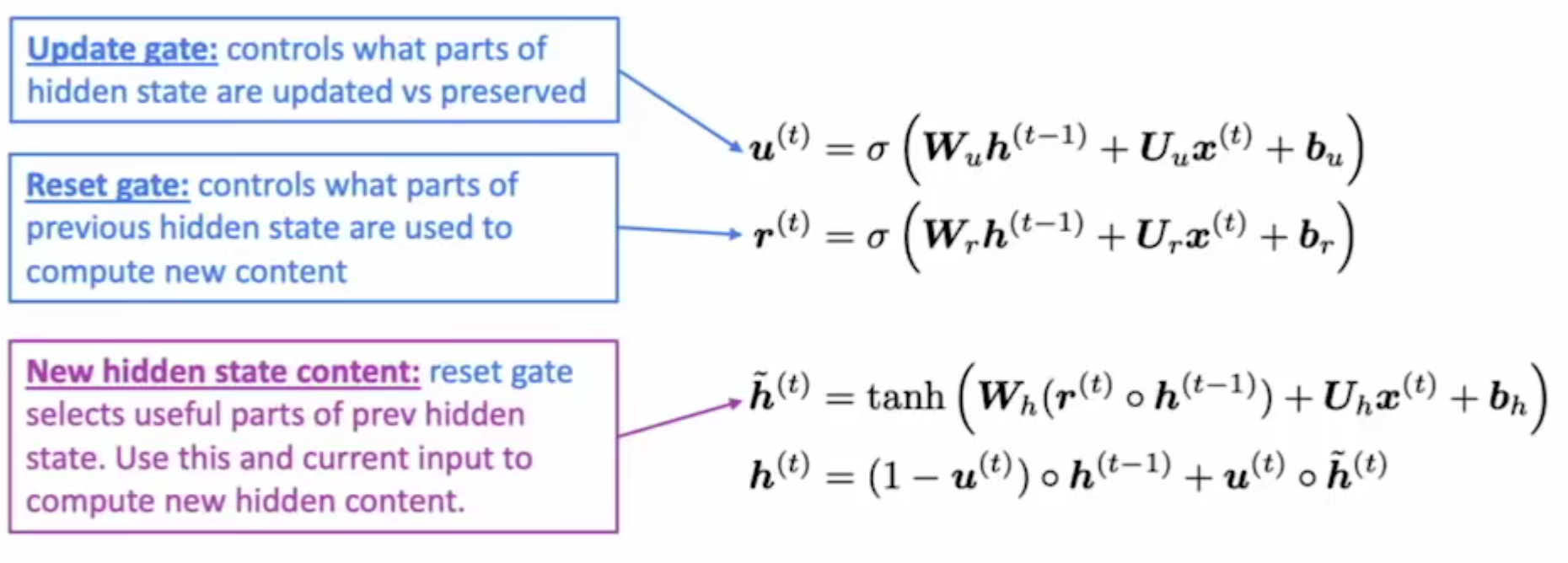
与LTSM应用效果区别不大,如果问题特别重视长距离信息的保存,默认使用LSTM
其他类型神经网络中同样存在梯度消失爆炸问题
随着网络层数的不断增加,梯度消失/爆炸更容易出现,导致深层神经网络的训练难度更高,出现了几种特殊类型网络,解决此类问题
resnet 残差网络
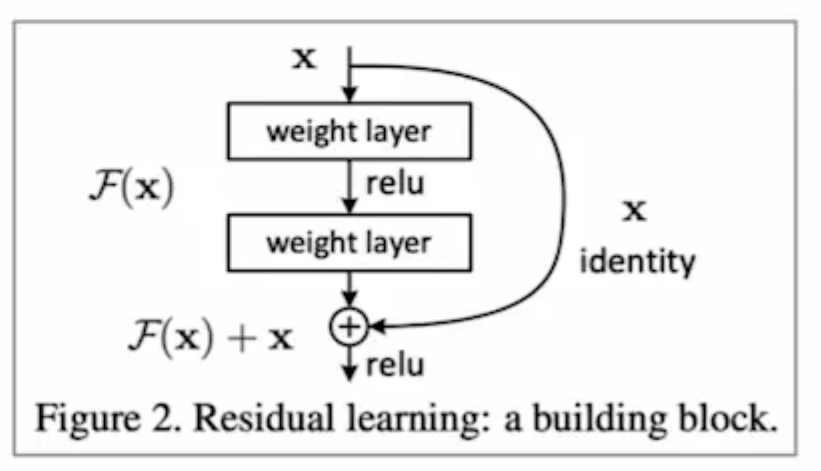
残差网络采用 shortcut-connection的思想,将几个layer成为block,假设每个block拟合函数为$F(x)$ ,目标函数为$H(x)$。传统网络思想通过不断训练用拟合函数$F(x)$映射目标函数$H(x)$,resnet将拟合目标修改为$H(x)-x$ ,在输出增加一个shortcut connection,直接将$x$ 加到拟合结果上,实现与传统网络相同的效果。
也正是因为shortcut connection的存在,实现了长距离信息的保存
densenet(待详细了解)
每一层的输入都包括前面所有层的输出
双向RNN(bidirectional)
为了解决单向RNN存在的句子歧义问题(I am terribly exciting 是难受 还是特别兴奋?),通过两个独立的RNN网络,分别正/逆输入句子,将两个网络相同词语获得的隐藏状态拼接,形成新的隐藏状态,输入到输入层获得输入结果。
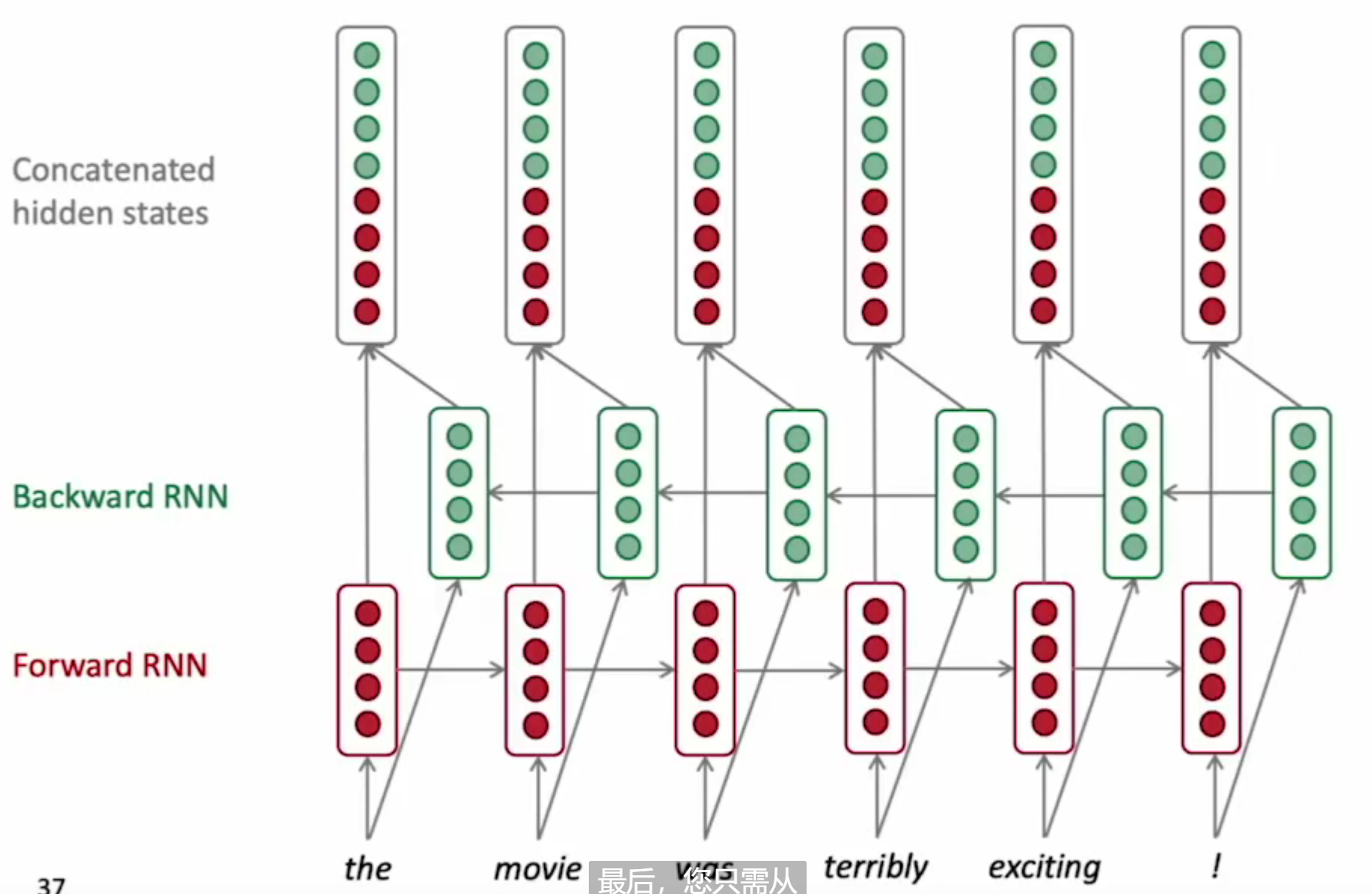
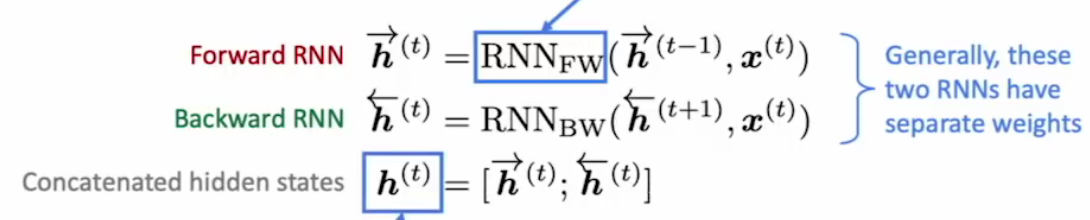
双向RNN的局限性
双向RNN只有在输入数据完整句子的情况下才能够使用,LM模型不适用。
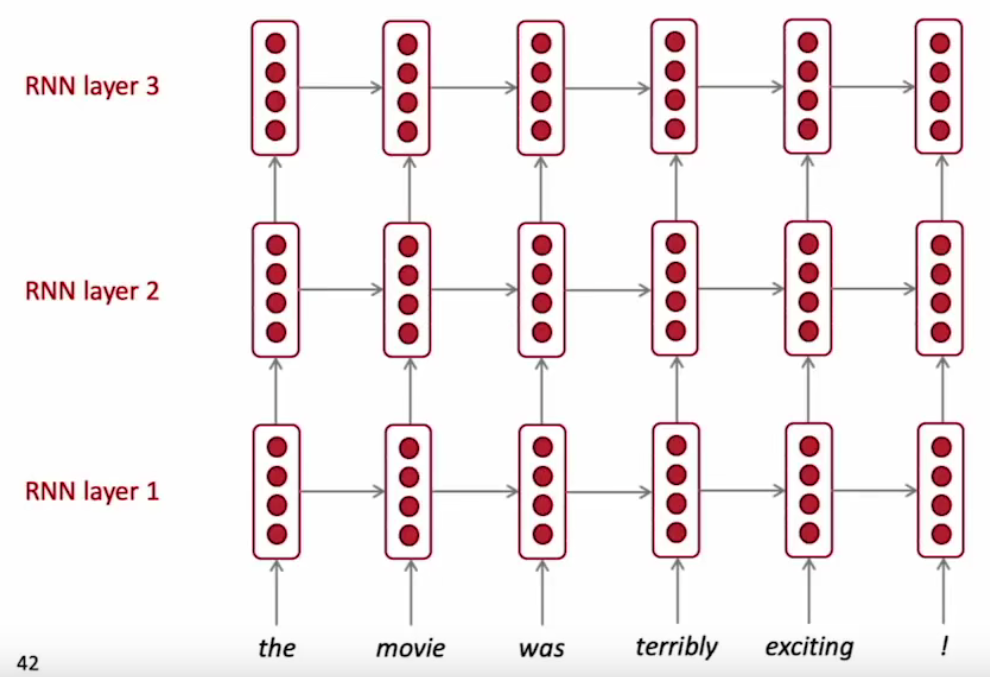
多层RNN(multi-layer)
多个RNN单元堆积在一起组成深度网络,类似于卷积网络的思想,通过增加网络的深度,实现从浅层特征学习=>深层特征学习。
总结