实用ML-5.偏差与方差

Bias & Variance

bias(偏差)：模型对于样本的拟合程度，模型输出结果与样本真实结果之间的差距，通过增加模型复杂程度，增加训练轮数，可以实现bias的降低，但可能会出现过拟合问题（high variance）

variance(方差)：模型预测结果的稳定性，通过简化模型，可以实现variance的降低 计算公式为 $E[(\hat y - E(\hat y)) ^ 2]$

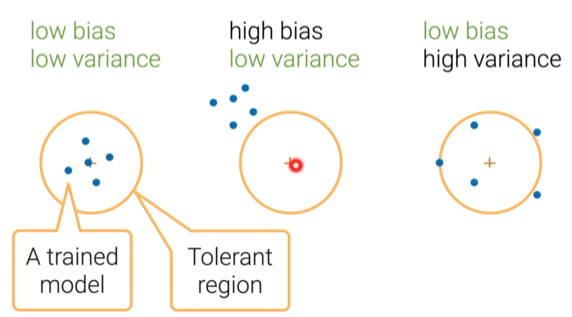
公式角度分析Bias 与 Variance

• 以MSE误差为例，计算bias和variance

  

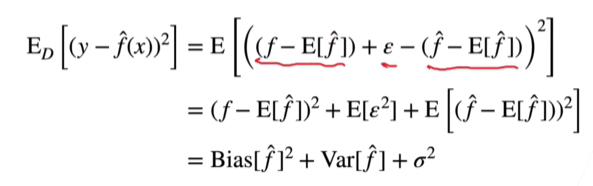
  • 在样本上求误差均值，首先将f展开为 $y = f +\epsilon$

  • 再在平方项内添加一个 y_hat期望 $E[\hat y]$

  • 由于 随机误差 $\epsilon$ 均值为0，方差为 $\sigma ^ 2$

    

  • 最终得到 Bias + Variance + $\sigma ^ 2$ 的形式

偏差与方差之间的关系

如何降低偏差和方差

• 集成学习可以同时降低两个误差