光与影的个人博客

NEUCoder

0%

读论文2-transformer

发表于 更新于 分类于 ，

Transformer

论文地址：Attention Is All You Need

本文提出一个区别于传统RNN、CNN的基于attention机制的网络架构-transformer，在具备RNN捕捉序列特征能力的基础上，实现了并行计算，降低了计算成本（看论文名字就知道作者对论文内容非常自信）

论文结构

总结下来发现这篇论文没讲故事，就是单纯的讲自己的工作，非常的简洁

  1. 摘要 abstract

    从问题提出->解决方案->效果，三句话介绍NMT->encoder-decoder->transformer模型，剩余的句子全在列举是实验效果，非常简洁

  2. 介绍 intro

    还是围绕着 rnn、encoder-decoder、attention这三个主要内容

    • 首先介绍rnn在LM和NMT中广泛应用，取得了SOTA成果，但是其还是存在无法并行计算的问题（介绍了为什么）
    • 然后介绍了attention机制能够跨距离建模依赖，但是目前研究大部分还是与rnn结合在一起
    • 最后引出了本文完全基于attention机制的transformer模型

  3. 背景 background

    • 列举了其他为了降低计算量的研究（convS2S, ByteNet）,但是降低效果不如transformer（证明自己工作的价值）
    • 通过列举参考文献，证明 self-attention，decoder-encoder两种设计的有效性（证明自己解决方案的科学性）

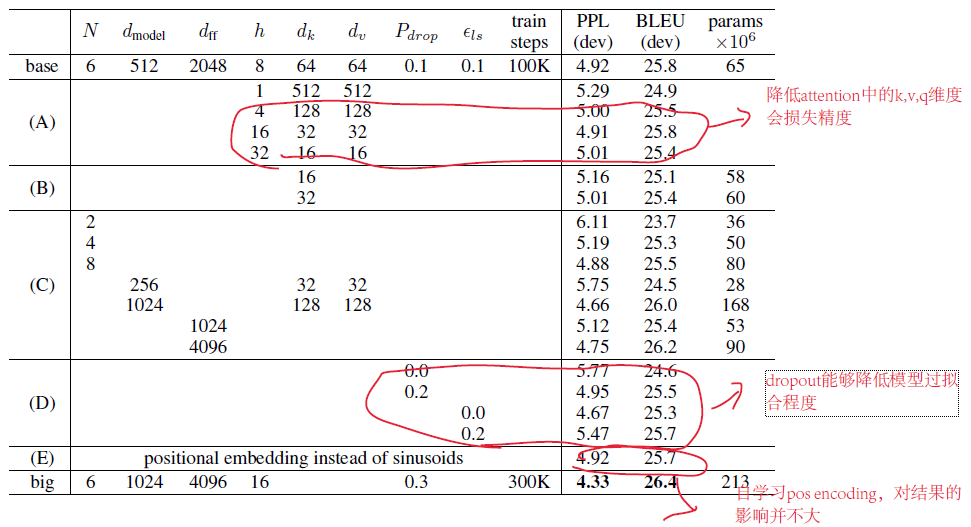
  1. 模型架构

    • 先是一段话+一张模型总图，整体介绍模型，然后每个层进行拆解，讲解内部机制
    • 总分结构

  2. why attention

    对比attention，rnn，cnn三种机制的计算的时间复杂度，证明attention机制真的有助于降低计算量

  3. 训练 traning

    介绍了训练参数等

  4. 实验 Results

    列举了在NMT以及English Constituency Parsing两个任务上的实验效果

    • WMT 2014 English-to-German，WMT 2014 English-to-French实现了SOTA
    • 为了证明transformer的在其它任务上的可泛化性，做了该实验，除了RNNG这个模型，transformer效果优于之前的所有模型

  5. 结论 conclusion

    总说自己提出了一个完全基于attention的模型，并再提了实验结果，最后说自己要把transformer推广到其他任务上（efficiently handle large inputs and outputssuch as images, audio and video）

模型结构

整体架构图如下，标准的encoder-decoder架构，encoder和decoder均为多个相同层的堆叠，其中encoder6层、decoder6层，共12层。

其他机制不再赘述，之前的博客总结过，简单总结一下几个新理解

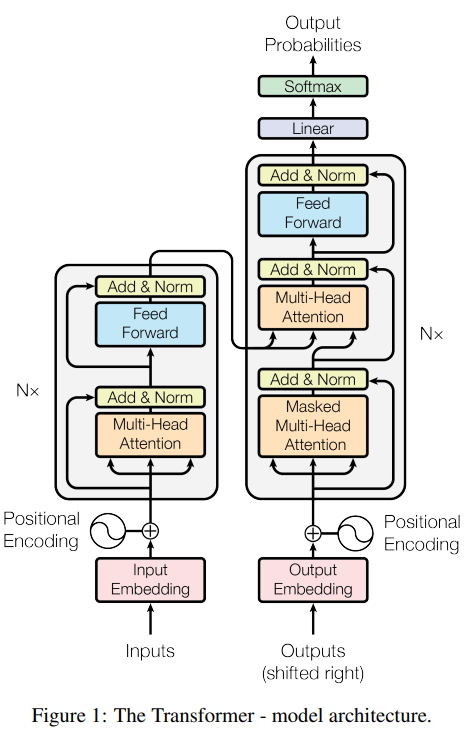
Scaled Dot-Product Attention

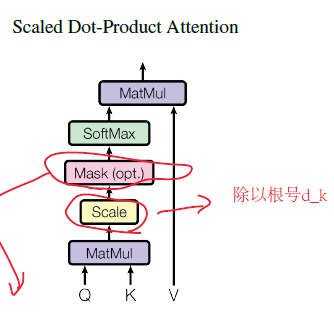
为什么要Scale？

We suspect that for large values of dk, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients[4]. To counteract this effect, we scale the dot products by $\frac{1}{\sqrt d_k}$

在计算注意力分数时，QK向量相乘后，要除以输入向量维度的平方根，此论文中给出的解释，当输入维度 $d_k$ 较大时，QK向量会变得相对较大，导致softmax函数落在图像两边（如下图），导致梯度过小（梯度消失），通过除以$\sqrt d_k$ 避免此问题的出现

encoder-decoder attention 的输入是什么

the queries come from the previous decoder layer,and the memory keys and values come from the output of the encoder.

query来自于decoder上一层的多头注意力机制输出，value和key来自于encoder的输出

多头注意力机制为什么有用？

类似于卷积神经网络中的通道的作用，不同的通道代表不同特征空间

embedding

为什么embedding层在+pos encoding前要乘以 $\sqrt d_k$?

随着输入维度的增加，嵌入向量的每个位置的数字会变小（总和接近于一），而pos encoding的大小不变，为了保持嵌入向量和pos encoding的相对大小关系保持不变，乘以 $\sqrt d_k$。

why self-attention?

原文中通过对比自注意力机制、卷积层、循环神经网络的计算复杂度、顺序计算量(是否可并行计算)、最大序列特征捕捉计算次数三个指标，证明自注意力机制在计算量上的优势

Complexity per Layer

  1. self-Attenion的主要计算量在 Q和V相乘，两个均为 $nd$维度矩阵，相乘复杂度为 $O(n^2d)$
  2. rnn每个时间步是一个输入为d,输出为d的全连接网络，整个seq的计算量为$O(n*d^2)$
  3. 卷积层与rnn类似，假设一维卷积核大小为k，每个元素近似在卷积核中卷积k次，整个seq的计算量为$O(knd^2)$
  4. 可见当n < d时，self-Attention的复杂度小于RNN

其他理解比较简单

实验参数

词嵌入

  1. WMT 2014 English-German 使用 byte pair encoding 做词典，共37000 个token
  2. WMT 2014 English-French 使用 32000 word-piece vocabulary

optimizer

使用Adam作为模型优化器

  1. 三个参数 $\beta_1=0.9,\beta_2=0.98,\epsilon=10^{-9}$

  2. 学习率如下，当训练步数小于warmup步数时，取 $step_num*warmup_steps^{-1.5}$,其中warmup取4000步

dropout

  1. 每个子层在残差相加之前，增加dropout
  2. pos encoding+embedding后增加dropout
  3. base模型的dropout概率为 $P_{drop} = 0.1$

label smoothing

训练时增加了标签平滑，参数值为 $\epsilon_{ls} = 0.1$