光与影的个人博客

NEUCoder

0%

基于统计的文档语义表示

发表于 更新于 分类于 ，

基于统计的文档语义表示

在深度学习模型到来之前，通常使用统计学方法获得表示的文档语义的特征向量，主要方法包括

  1. TF-IDF
  2. 基于SVD分解的LSA（潜在语义索引/分析 Latent Semantic Indexing/Analysis）
  3. LDiA 隐形迪利克雷分布

其中前两种分布理解较为简单，LDiA涉及比较多的概率分布知识

TF-IDF

term frequency–inverse document frequency，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加（TF），但同时会随着它在语料库中出现的频率成反比下降（IDF）

TF

term frequency，给定一个词，当前词在当前文件出现的频率（通常需要除文档长度），计算公式如下

IDF

inverse document frequency，给定一个词，IDF值为文档库中总文档数除以包含该词的文档数

将两个值相即为当前文档中该词的TF-IDF值，计算文档在词表上所有词的TF-IDF值，即可获得相较于词袋向量更加稠密但维度相同的文档特征向量,TF-IDF作为语义特征向量还存在着一些问题

  1. 无法解决不同拼写但意思相近的词，TF-IDF计算是会将其看作不同的特征
  2. TF-IDF特征向量的维度还是过大，计算量大且在样本量小（维度与样本数量接近）的时候，容易出现过拟合
1
2
3
4
# 快速计算TFIDF值，问题是处理不了中文
sklearn.feature_extraction.text.TfidfVectorizer
# 将词频矩阵快速转化为IDF值（中文只能用这个了）
sklearn.feature_extraction.text.TfidfTransformer

LSA 潜在语义分析

LSA实际上就是SVD矩阵分解应用到NLP领域中换的一个名字，结合SVD和PCA对别进行理解

SVD

常用的针对非方阵矩阵的一种分解方法

其中矩阵 U和V满足:

迁移到NLP领域中,使用截断的SVD分解（取前p大的奇异值）,定义为所谓的潜在语义主题

  • 矩阵$M_{mn}$为 **词 文档** 的特征向量矩阵，每一列均为一篇文档的特征向量
  • 矩阵 $U_{mp}$ 为 **词 潜在语义主题** 的关系矩阵
  • 矩阵 $V_{np}$ 为 **文档 潜在语义主题** 的关系矩阵

通过矩阵分解，获得了文档的潜在语义主题表示，实现了文档特征向量的降维（从词维度降低到定义的主题维度）

PCA

Principal Component Analysis，从降维的角度出发，发现PCA与SVD都是在做类似于矩阵分解的操作，实现降维的目的。PCA出发点为找到对$X$的一种降维方法$Y=WX$，使得损失的信息量最少，如何实现这个目标？

  1. 降维后某个特征（或者说维度）的方差最大（组内多样化）
  2. 不同特征之间的协方差为0（组间相关性尽量小）

根据降维要求和方差大小，舍弃较小方差特征，保留较大方差特征，实现降维。

  • 如何转化为数学问题求解？引出了协方差矩阵，上述两个目标即为将协方差矩阵相似对角化过程（非对角线元素（协方差）转化为0，对角线元素（方差）转化为特征值）
  • 如何快速找到目标矩阵 $X$ 的协方差矩阵？当$X$不同特征内归一化处理后，$XX^T$即为协方差矩阵

最终转化为求解 $XX^T$的特征向量矩阵 $W$

PCA VS SVD

经过分析两者均最终转化为了 $XX^T$的特征向量矩阵的求解过程，两者在计算上实际等价，不同点在于

  1. PCA目的为降维，SVD目的为分解
  2. PCA只能应用于方阵，SVD均可
  3. PCA需要对数据进行中心化处理

sklearn中的PCA实际上就是用SVD方法求解的

1
2
3
4
5
6
7
8
# 截断SVD
sklearn.decomposition.TruncatedSVD([n_components, ...])
# PCA
sklearn.decomposition.PCA([n_components, copy, ...])
# 增量PCA 解决数量过大内存不足问题的近似PCA
sklearn.decomposition.IncrementalPCA([n_components, ...])
# 稀疏PCA
sklearn.decomposition.SparsePCA

LDiA

Latent Dirichlet allocation 隐含迪利克雷分布，即它认为一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。过程涉及到两个分布关系

  1. 文档的主题分布
  2. 每个主题的词分布

LDiA假设这两个分布均满足多项式分布，其中多项式参数个数为主题个数和词个数，在此假设下，我们已知数据+分布，如何求出目标分布的参数？LDiA假设主题分布和词分布的先验分布均为Dirichlet分布，即

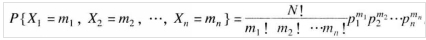
  1. 文档主题多项式分布参数 $p_1,p_2,p_3….p_n$满足Dirichlet分布（$p_i$ 为某文档中 $topic_i$ 出现的概率）
  2. 主题词多项分布 $p_1,p_2,p_3….p_n$满足Dirichlet分布（$p_i$ 即为某主题中 $word_i$ 出现的概率）

常用方法有下面两种，不太清楚是否与贝叶斯估计有关系（不深入了解了，浪费时间也没必要）

  1. EM算法
  2. Gibbs Sampling算法

想到了上学期学的贝叶斯估计求未知参数

我想到了数理统计里的贝叶斯估计，通过先验分布和后验分布，可以得到参数关于样本的概率分布，公式如下(应用数理统计-孙荣恒)

其中 $y$ 后验分布中的未知参数，$\pi(y)$ 为先验分布（LDiA中的Dirichlet分布），$f(x_1,…,x_n|y)$ 为后验分布（LDiA中的多项式分布），得到未知参数关于实验数据（输入文档）的分布后，采取特定方法即可求得未知参数的估计值

简单总结

根据上述分析，我们可以得到LDA输入有两个超参数

  1. 文档-主题先验Dirichlet分布的参数
  2. 主题-词先验Dirichlet分布的参数

LDA实际在求解的参数为

  1. 文档-主题多项式分布的参数
  2. 主题-词 多项式分布的参数

参考

  1. tf-idf
  2. 奇异值分解
  3. 隐含狄利克雷分布
  4. NLP-04 隐含狄利克雷分布(LDA)
  5. 应用数理统计-孙荣恒