搜索算法整理

搜索相关算法

开头废话：最近这几周搞辣鸡项目花了太长时间，好久没写博客了，整理一下这几周写的搜索算法

通过枚举遍历问题的解空间，实现问题的求解，搜索作为比较基础的算法问题之一，题目数量众多，问题难度可难可易，希望通过这篇博客的整理能够加深我对目前学习到的相关搜索算法的理解。

主要的算法

1. DFS 深度优先搜索
2. BFS 广度优先搜索
3. 双向搜索
4. Best First Search 最佳优先搜索
5. 迭代加深搜索
6. 其他

基础搜索算法

最简单也是最常用的两个搜索算法（简单总结）

1. 深度优先搜索
   • 每次递归首先尝试向更深的结点走
2. 广度优先搜索
   • 每次枚举穷尽同一层的所有结点

其中深度优先搜索更适合搜索解空间深度与目标解深度相近类型问题，广度优先遍历更适合搜索目标解深度一定程度小于目标解深度类型问题

双向搜索

与普通DFS和BFS不同的点在于，双向搜索同时从两个”方向“开始搜索，这里的方向包括两种形式

1. 从初始状态正向搜索+目标状态逆向搜索
2. 将问题划分为两个规模为一半的子问题，分别进行搜索（meet in middle）

双向搜索能够使得遍历解空间数量在幂级上缩小一半

正/逆双向搜索（BFS）

基于BFS正/逆双向搜索，问题需要满足目标解已知，否则无法进行双向搜索，以深度为N的二叉问题为例

• 若使用普通的BFS，找到解的BFS深度为N，时间复杂度为O(2^N)

• 双向bfs每次从初始状态和目标状态遍历深度加一，相当于两个深度为N/2的BFS，时间复杂度为0(2^(N/2))

伪代码模板（自己写的）如下：

• 两个访问标记，两个队列

• 每次训练，正向bfs一层，逆向bfs一层

• 终止条件：正/逆向bfs过程中，新状态存在于另一个方向的访问标记中；或队列为空

  //主函数每次循环，正向和逆均搜索一层
  for (int i = 0; !forwardQue.isEmpty() || !backwardQue.isEmpty(); i++) {
              //正向搜索一层
              if (!forwardQue.isEmpty() && bfs(forwardVisitedMap, backwardVisitedMap, forwardQue, i)) return;
              //逆向搜索一层
              if (!backwardQue.isEmpty() && bfs(backwardVisitedMap, forwardVisitedMap, backwardQue, i)) return;
  }
  //修改终止条件的bfs
  bfs(forwardVisitedMap, backwardVisitedMap, forwardQue, int curDepth) {
          int tempSize = forwardQue.size();
          for (int j = 0; j < tempSize; j++) {
              curState = forwardQue.poll();
              //遍历所有子状态
              for(childState of curState){
                  //若逆向的map中包含当前状态，说明双向搜索相交，找到最优解
                  if(backwardVisitedMap.contains(childState)){
                      //记录或者输出解空间
                      return true;
                  }
                  //否则按照普通的bfs继续执行
                  if(!forwardVisitedMap.contains(childState)){
                      forwardVisitedMap.put(childState， curDepth);
                      forwardQue.offer(childState)
                  }
              }
          }
          return false;
  }

例题：

• P1032 [NOIP2002 提高组] 字串变换 BFS VS 双向BFS

  • 时间空间复杂度均降低
  

Meet in middle

将规模为N问题，从中间拆分为两个N/2子问题，两个子问题分别进行dfs+状态存储，最后两个状态组合求解，已N个物品的背包问题为例

• 与双向dfs相同，时间复杂度从 O(2^N)降低到0(2^(N/2))
• 空间复杂度由于要存储中间状态，最坏情况下为0(2^(N/2))

这类问题的难点其实在判断直接暴力是否超时

• 一般刷题平台的时间限制是1秒或2秒，操作次数应该控制在 $10^{7-9} \approx 2^{23-25}$ 左右（按照这个标准进行判断）

伪代码模板：

• 另一种解法时前后dfs获得的状态均存下来，最后一块求解（我觉得空间复杂度太大，没用过）

 public static void dfs1(depth, status){
     //到中间停止dfs
     if(depth == N / 2){
         //不需要state，只需要value 直接存储在列表
         states.add(value)
         //需要记录状态的数组或者Map中
         states[status] = value
         return;
     }
new_status = //根据规则+status确定新的status
     dfs1(depth + 1, new_status);
 }

 public static void dfs2(depth, status){
     //到N国模
     if(depth == N){
         //找到states数组中需要的value+当前dfs结果组成目标解
        	//可能会用到：二分查找
     }
     return  dfs1(depth + 1, new_status);
 }

 public static void main(String[] args) {
     //首先第一个dfs，求前半部分状态
     dfs1(0, 0);
     //第二个dfs求第二部分状态，同时与第一个部分状态组合形成解
     dfs2(N/2);
 }

例题：

• AcWing171. 送礼物
  • 暴力：$O(2^{46})$ 动态规划：$O(46*2^{31}) $ 明显超时
  • 双向DFS：$O(2^{23})$
• P3067 [USACO12OPEN]Balanced Cow Subsets G
  • 暴力：$O(2^{40})$ 动态规划：$O(40*2^{18}) $ 明显超时，且动态规划方法会超内存
  • 双向DFS：$O(2^{20})$
• P3067 [USACO12OPEN]Balanced Cow Subsets G（知识点比较全的一道题 重点！！！）
  • 这道题双向DFS：$O(3^{20}) \approx O(10^{9})$
  • 使用二分查找搜索状态会导致时间复杂度增加一个数量级超时，map存储状态

Best First Search 最佳优先搜索

最佳优先搜索是一种结合了贪心的搜索思想：如果任意时刻能够近似估计到达目标点的成本，每次选取最底层进行扩展搜索，以降低搜索空间。主要的搜索算法有

1. Greedy/Beam Search
   • 最简单应用贪心思路到搜索上的算法，每次扩展选择估计成本最低的结点加入到路径中（多个就是beam search）
   • 这种方法简单且暴力，但是存在贪心算法的普遍问题，即可能无法找到最优解
2. Dijkstra’s algorithm
   • 每次选择距离出发点成本最低的点进行扩展
   • 能够保证找到最优解，但是搜索复杂度还是较高（剪枝效率不高）
   • 采用了堆优化的算法时间复杂度为 $O(E + V logV)$，空间复杂度为 $O(logV)$（其中 $E$ 为边数，$V$为结点数量）
3. A* algorithm
   • A 算法类似于Dijkstra，只是Dijkstra会获得从出发点到所有目的地的最短路径生成树，A只会找到出发点到目标点的最短路径

A*算法

Peter Hart, Nils Nilsson and Bertram Raphael of Stanford Research Institute (now SRI International) first published the algorithm in 1968. [4] It can be seen as an extension of Dijkstra’s algorithm. A* achieves better performance by using heuristics) to guide its search.

A*算法是对Dijkstra’s algorithm的扩展，A* 定义了特殊形式的函数$f(n)$作为结点优先级的衡量标准

$$f(n) = g(n) + h(n)$$

其中$g(n)$ 为起点到结点n的成本（已知），$h(n)$为结点n到终点成本的估计函数（对未知的估计）-启发函数

启发函数（heuristic function）

其实仔细看看我们会发现，其实A*算法相较于Dijkstra只是增加了一个启发函数$h(n)$，为什么要添加启发函数？

1. “以史为鉴” $g(n)$ ：从结点到当前节点的成本我是已知的，所以每次选成本最低的可能能找到最优解（Dijkstra）
2. “最速梯度下降” $h(n)$：如果我能够近似估计从当前结点到目标结点的距离，我肯定要选择估计上更近的点，更可能找到最优解（Greedy Search）

所以启发函数的选取对于A*算法极为重要

1. 一方面决定剪枝效率
2. 一方面决定能够A*能否找到最优解

论文中证明了只要启发函数满足以下两个性质即能满足我们的要求

1. admissible：$h(x) \leq h^(x)$ 其中 $h^(x)$ 为到目标结点的真实距离，即到目标结点的估计距离非严格小于实际距离
2. consistent/monotone：若存在边$(x, y)$，则 $h(x) ≤ d(x, y) + h(y)$，即当前节点到目标结点的估计距离，小于当前结点到临接结点的距离+临接结点到目标结点的估计距离（可以理解成 两边之和大于第三边）
3. 若启发函数满足admissible，则A算法一定能够找到最优解；若启发函数满足consistent，则A\算法不会向优先队列中重复添加点（即单调递增，后找到点的f(n) 一定小于前找到点），其中consistent性质蕴含admissible，若启发函数具有consistent，其一定满足admissible性质

根据wiki百科中的解释简单理解一下两个性质为什么导致结果成立

1. admissible $\rightarrow$ 能够找到最优解：反证法，由于最后一次目标结点进入队列时其 $f(n_{目标}) = g(n_{目标}) + (h(n_{目标}) = 0)$, 其函数值已不包括估计值，假设我们找到非最优解，则存在一条到目标点的路径长度小于A迭代退出时选择的路径，取该路径上的任意一点 $n_{rand}$ ，其启发函数一定满足$f(n_{rand}) = g(n_{rand}) + (h(n_{rand}) < 经过n_{rand}实际路径长 < f(n_{目标}))$，所以优先队列不可能弹出目标结点，A\此次迭代优先队列不可能弹出目标节点。
2. consistent $\rightarrow$ admissible：随便选一条从出发点到目标点的路径，根据 $h(x) ≤ d(x, y) + h(y)$ 不断的转换不等式: $h(x) ≤ d(x, y) + h(y) \leq d(x, y) + d(y, z) + h(z)…$ 直到不等式转换为$h(x) ≤ d(x, n_{目标})$，推导出admissible

常用的启发函数有（别人的博客）

所以如何选择启发函数？

1. 首先要满足admissible的性质，保证算法能够找到最优解
2. 其次启发函数的估计值尽量大，
3. 极端情况（即$h(x) = h^(x)$）下，A算法转化为 保证能够找到解的贪心搜索；若 $h(x) = 0$，A算法转化为 *Dijkstra算法

复杂度

1. 时间复杂度：看不明白证明
2. 空间复杂度：看不明白证明

伪代码模板

在Dijkstra改改就是A*（不会写伪代码，网上抄一个）

* 初始化open_set和close_set；
* 将起点加入open_set中，并设置优先级为0（优先级最高）；
* 如果open_set不为空，则从open_set中选取优先级最高的节点n：
    * 如果节点n为终点，则：
        * 从终点开始逐步追踪parent节点，一直达到起点；
        * 返回找到的结果路径，算法结束；
    * 如果节点n不是终点，则：
        * 将节点n从open_set中删除，并加入close_set中；
        * 遍历节点n所有的邻近节点：
            * 如果邻近节点m在close_set中，则：
                * 跳过，选取下一个邻近节点
            * 如果邻近节点m也不在open_set中，则：
                * 设置节点m的parent为节点n
                * 计算节点m的优先级
                * 将节点m加入open_set中

典型例题

1. P1379 八数码难题
   • 比较了几个不同的启发函数计算方式，确实是启发函数越大，剪枝效果越好

迭代加深

通过限制DFS搜索的深度实现BFS效果，本质上还是DFS搜索，只是每次DFS增加了最大递归深度。

• 当DFS达到最大深度时，即使未找到目标解，也要返回。
• 若某次深度d的DFS没有找到解，则将迭代深度+1，重新进行DFS搜索。

伪代码如下:

for(int maxDepth = 1;maxDepth <= 最大迭代深度；maxDepth++){
	dfs(0, maxDepth)
}
dfs(depth, maxDepth){
	if(depth == maxDepth){
		return;
	}
	dfs(depth + 1, maxDepth)
}

迭代加深与BFS的区别在于

1. 迭代加深方法通过DFS实现BFS效果，避免了BFS队列对于状态的存储，降低了空间占用
2. 每次增加迭代深度，会导致DFS重复遍历

什么时机使用迭代加深？（玄学）

• 当搜索树的分支比较多时，每增加一层的搜索复杂度会出现指数级爆炸式增长，这时前面重复进行的部分所带来的复杂度几乎可以忽略

• 为了避免过量的空间占用，采用迭代加深

• 题目特征：限定了搜索深度，要求找到解没有限定解的类型（遇到这样的题，就嫁了吧）

典型例题

单纯的迭代加深方法应用的不多，与A算法结合使用IDA\的比较多

1. 170. 加成序列
   • BFS的最坏空间复杂度为O(N!),当N=100时，对应复杂度能达到 $10^{158}$
   • 迭代加深重复遍历相较于状态个数已经可以忽略不计

IDA*

迭代加深和A*结合，使用启发函数在dfs过程中减枝，从而实现算法时间复杂度的降低，伪代码如下：

for(int maxDepth = 1;maxDepth <= 最大迭代深度；maxDepth++){
	dfs(0, maxDepth)
}
dfs(depth, maxDepth){
	if(depth == maxDepth){
		return;
	}
	//只有在启发函数+当前代价小于最大代价时才继续进行迭代
	if(depth + h(curStatus) <= maxDepth)
		dfs(depth + 1, maxDepth)
}

观察代码其实和迭代加深算法区别不大，只是增加了减枝函数，最难的点也就在如何决定这个剪枝函数-启发函数的选取，

典型例题

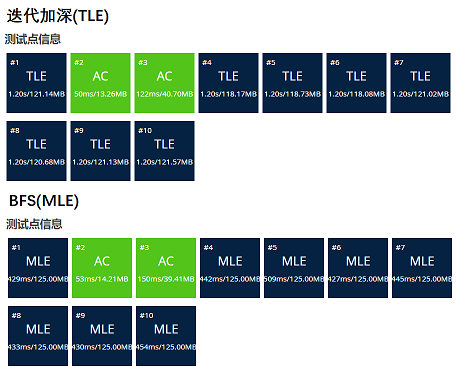
1. P2324 [SCOI2005]骑士精神， 简单分析一下为什么要用IDA*

   • 类似于八数码难题，从空位置出发，每次寻找能够移动到

   • 空位置的棋子，该问题每次最多可能有8个位置能够移动到空位置

   • bfs和迭代加深算法的最坏复杂度为O(8^15)（限制了递归深度最大为15），显然超时，且BFS还会出现MLE问题，所以只能尝试IDA*

     

2. P2534 [AHOI2012]铁盘整理

   • IDA*的模板题目，难点是想出来启发函数，其他倒不难

Dancing Links

OIWIKI:Dancing Links

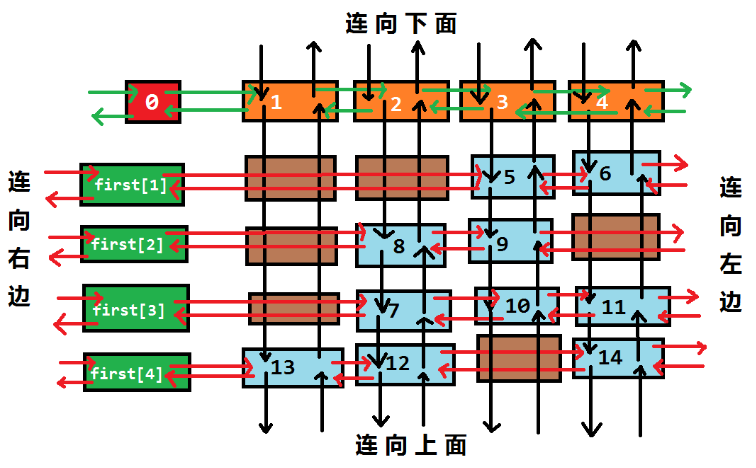
舞蹈链是为了解决精确覆盖的一种特殊数据结构，精确覆盖问题目前只能通过暴力回溯法的方式实现求解，Dancing links通过链表存储的方式实现了时间和空间复杂度一定程度的降低（难度太大找工作用不到，了解一下，不深入学习，贴张别人的图表示字自己学习过了）

总结

算是把搜索问题的主要解题思路整理学习完毕，搜索问题的难点可以总结为：

1. 剪枝：无论是普通的DFS还是A，IDA\算法，实现难度其实都不是很大，最难的点还是在于找到合适的剪枝函数
2. 时间空间复杂度分析：很多时候问题的方法显而易见，难点反而在选用什么搜索方法才能适应题目的时间空间复杂度要求
3. 问题抽象：如何讲问题转化为搜索问题是比较难的点，很多问题往往即使告诉你要用搜索（比如铁盘整理和骑士精神），我也会想不明白

其他没什么可总结的了，其实目前很多算法只能说懂了怎么写，真正的解决相关搜索问题的能力还欠缺，继续努力！！！

相关参考

1. OI WiKi的搜索专题
2. luogu官方搜索题单
3. wikipeida A*_search_algorithm
4. 博客：跳跃的舞者，舞蹈链（Dancing Links）算法——求解精确覆盖问题
5. 部分题目：acWing