光与影的个人博客

NEUCoder

0%

线段树整理

发表于 更新于 分类于 ，

线段树总结

学完树状数组，很难控制住自己不学线段树，线段树是一种可以在$O(logN)$ 时间复杂度内实现区间和单点操作的数据结构：

  1. 单点修改/查询
  2. 区间修改/查询

与树状数组的区别在于：树状数组只能执行 单点修改+区间查询 或 区间修改+单点查询 。线段树能够均能支持，但是复杂度的常数系数显著大于树状数组（ps:能用树状数组就用树状数组）

线段树从何而来？我的简单理解

  1. 对于区间修改和区间查询，最朴素的思想就是遍历区间元素逐个修改，然而朴素的复杂度是我们无法接受的，所以我们如何改进？自然而然想到通过空间换时间的想法，通过提前存储要修改查询的“区间”，降低修改和查询的复杂度。由此我们确定了要“存区间”
  2. 然而如何 “存区间”？每次查询和修改的区间左端点和右端点都是任意的，不可能把所有可能的左右端点组成形成的区间存下来，根据区间之间的重叠性质，我们能够想到：既然无法存储所有的区间，不如存储一定数量不重叠的区间，只要这些区间能够拼接出所有的目标区间即可，问题就变成了怎么拆分区间？
  3. 如何设计存储的现成区间？每次寻找给定一个区间，寻找已经存储的现成区间进行拼接，我们的目标自然而然是 拆分的次数越少越少（最好是我直接存了这个区间），这个拆分次数最少，自然而然想到，对 最大区间进行二分拆分，以树的形式进行存储，这样拆分次数最坏就是存储树的高度（这一步逻辑还是有点问题）
  4. 最终我们得到了线段树这一个存储结构

线段树定义

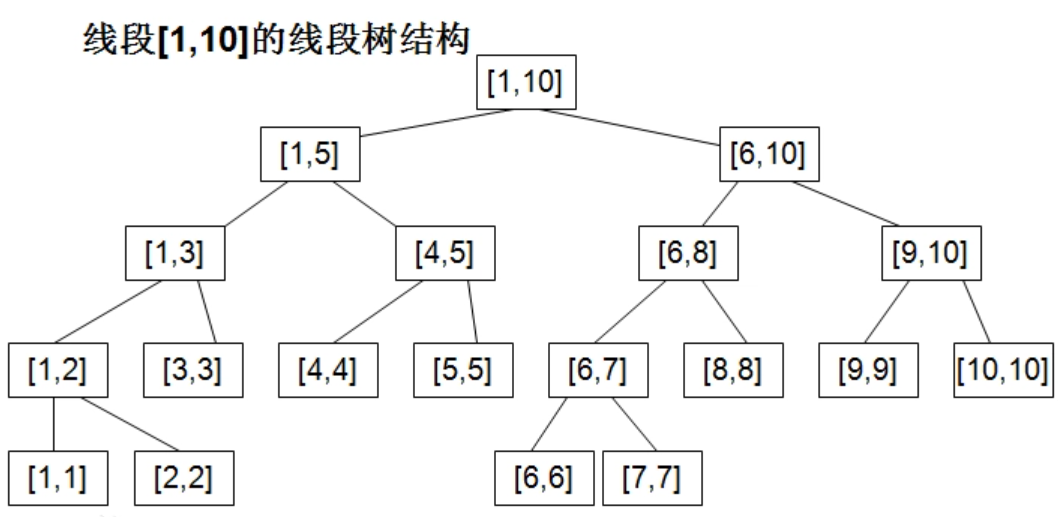
如下图所示，线段树每个结点对应一个区间，每个长度不为1的区间的结点包括两个子节点（划分为两个子区间），叶子节点为长度为1的区间。

  • 每个结点维护区间信息，例如区间和、最值等
  • 通过递归修改查询等可以快速实现区间操作
  • 线段树每次分裂两个子节点区间长度缩小两倍，所以线段树理想情况下为完全二叉树，普通情况下为近似完全二叉树，所以即可以使用树的方式存储，也可使用完全二叉树数组形式村存储

建树

建树代码如下：

  • 时间复杂度和线段树结点个数,空间复杂度为栈深度

  • 空间复杂度： $log_2n$

  • 时间复杂度： $2^{log_2{n} + 1} - 1 \approx 4 n$ (若使用二叉树数组存储，空间直接开4 * n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private void buildTree(int curPos, int left, int right, int[] aimArray){
    /*
     * 建立线段树（区间和）
     * 1. 空间复杂度：o(4 * N)
     * 2. 时间复杂度：o(4 * N)
    * */
    if(left == right){
        //当前区间长度为1，叶子节点
        heapArray[heapPos] = aimArray[left];
        return;
    }
    int mid = left + (right - left) >> 1;
    //区间分裂，左节点+右节点
    buildTree(curPos * 2, left, mid, aimArray);
    buildTree(curPos * 2 + 1, mid + 1, right, aimArray);
    //当前区间和等于两个子区间和求和
    heapArray[curPos] = heapArray[curPos * 2] + heapArray[curPos * 2 + 1];
}

更新

更新代码如下：

  • 若每次更新修改所有包含当前结点的区间，时间复杂度将远超目标复杂度，在实现过程中引入了”懒标记”
  • 当修改某个结点时，不递归修改当前结点的孩子节点，而是将当前结点的”懒标记”，在下次修改或者查询涉及到当前节点，再进行“修改”（这里的修改时特殊的修改，即修改孩子结点，并将懒标记下推到孩子结点）- pushdown
  • 通过“懒标记”确保了，更新的时间复杂度为O(logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
private void pushDown(int heapPos, int left, int right){
    if(lazyLabel[heapPos] != 0){
        int mid = left + ((right - left) >> 1);
        //首先将积累的更新修改到孩子节点
        heapArray[heapPos * 2] += (mid - left + 1) * lazyLabel[heapPos];
        heapArray[heapPos * 2 + 1] += (right - (mid + 1) + 1) * lazyLabel[heapPos];
        //孩子结点记录"懒标签",下一次遍历到孩子结点继续下推
        if(mid != left){
            lazyLabel[heapPos * 2] += lazyLabel[heapPos];
        }
        if(mid + 1 != right){
            lazyLabel[heapPos * 2 + 1] += lazyLabel[heapPos];
        }
    }
    //清除当前结点的"懒标签"
    lazyLabel[heapPos] = 0;
}

private void update(int heapPos, int left, int right, int leftRange, int rightRange, int value){
    //当更新范围大于当前范围时，直接修改，并记录懒标记
    if(leftRange <= left && rightRange >= right){
        heapArray[heapPos] += (right - left + 1) * value;
        //叶子节点不标记
        if(right - left != 0){
            lazyLabel[heapPos] += value;
        }
    }
    else{
        //下推（
        pushDown(heapPos, left, right);
        //向下更新
        int mid = left + ((right - left) >> 1);
        //左节点区间交叉
        if(mid >= leftRange){
            update(heapPos * 2, left, mid, leftRange, rightRange, value);
        }
        //右节点区间交叉
        if(mid <= rightRange){
            update(heapPos * 2 + 1, mid + 1, right, leftRange, rightRange, value);
        }
        //更新当前区间值
        heapArray[heapPos] = heapArray[heapPos * 2] + heapArray[heapPos * 2 + 1];
    }
}

查询

查询代码如下：

  • 会写更新就会写查询，而且查询比更新还要简单
  • 时间复杂度为O(logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private int query(int heapPos, int left, int right, int leftRange, int rightRange){
    if(leftRange <= left && rightRange >= right){
        return heapArray[heapPos];
    }
    //首先pushDown
    pushDown(heapPos, left, right);
    //区间拆分
    int result = 0;
    int mid = left + ((right - left) >> 1);
    //与左节点区间有交叉
    if(mid >= leftRange){
        result += query(heapPos * 2, left, mid, leftRange, rightRange);
    }
    //与右节点区间有交叉
    if(mid < rightRange){
        result += query(heapPos * 2, mid + 1, right, leftRange, rightRange);
    }
    return result;
}

线段树例题

套模板

  1. 洛谷 P2357 守墓人 状态为和
  2. 洛谷 P3870 [TJOI2009] 开关 状态为值为1的个数
  3. 洛谷 P3373 【模板】线段树 2 两种区间修改操作
    • 难点在于 lazylabel的设计

特殊区间状态

  1. lc 218. 天际线问题 每个区间代表线段（不再是离散的点）

    • 扫描线+线段树，这里每个区间不再是每个点的集合，而是真正的线段

      1. 建树修改，左区间的右端点与右区间的左端点相同（线段一分为二，不再是点一分为二）

        1
        2
        3
         //区间分裂，左节点+右节点
        buildTree(curPos * 2, left, mid, aimArray);
        buildTree(curPos * 2 + 1, mid, right, aimArray);

      2. 更新/查询修改，去掉了等号（线段相交，端点重合不叫线段相交）

        1
        2
        3
        4
        5
        6
        7
        if(mid > leftRange){
            update(heapPos * 2, left, mid, leftRange, rightRange, value);
        }
        //右节点区间交叉
        if(mid < rightRange){
            update(heapPos * 2 + 1, mid, right, leftRange, rightRange, value);
        }

    • 好玩的一点，这个题目不需要pushdown（因为查询只查根节点不需要pushdown，且lazylabel记录覆盖次数无法pushdown）

  2. P2003 [CRCI2007-2008] PLATFORME 平板

    • 与上一道题类似，更简单，都是存储线段

参考

  1. OIWIKI 线段树
  2. 百度百科：线段树
  3. 洛谷：线段树模板题